Start » Exercises » Engineering Mechanics I » Determine the required static friction

Determine the required static friction

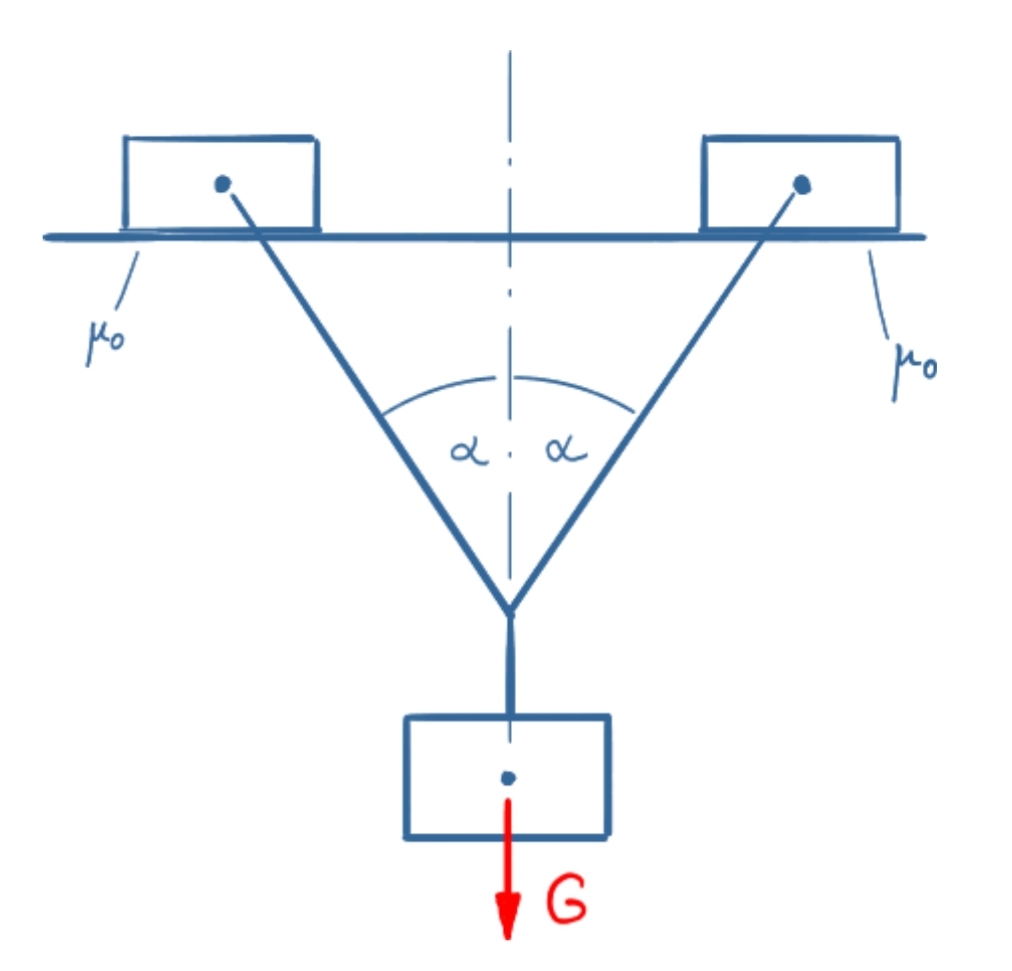
Task

A weight G pulls symmetrically on two sliding carriages at the angle alpha. What is the minimum static friction required for equilibrium to prevail? The dimensions of the slide can be neglected here.

Slide carriage at rest
Slide carriage at rest

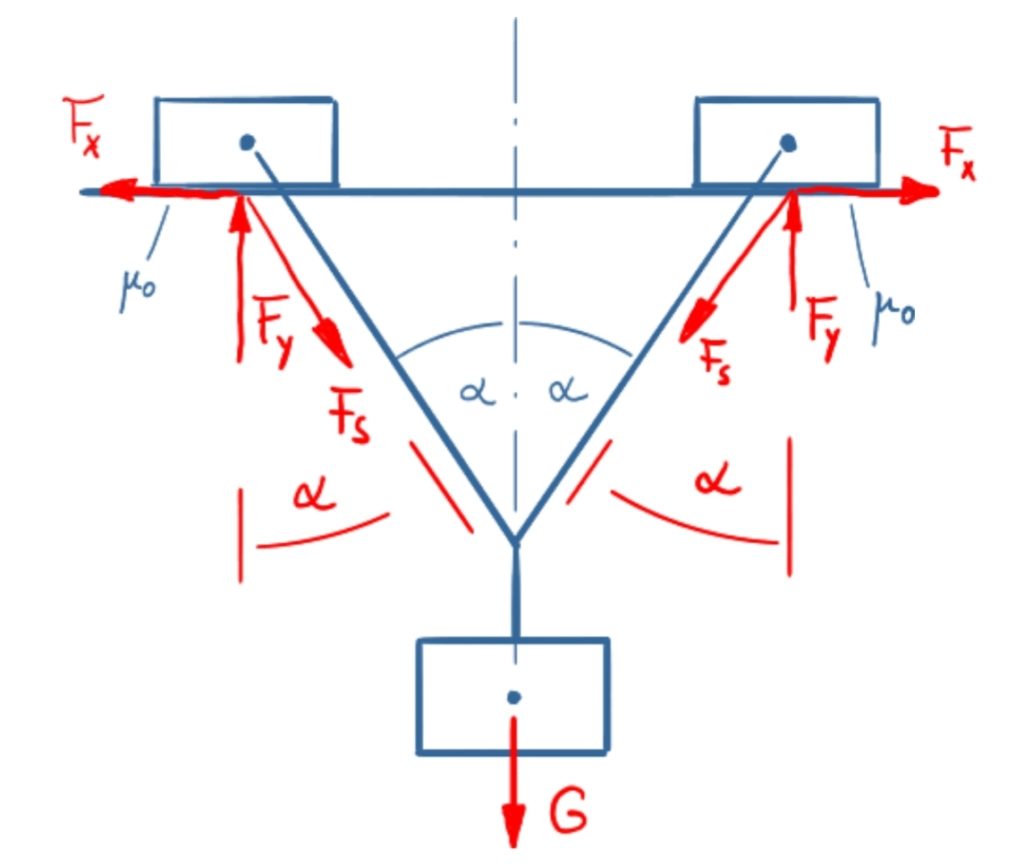
Solution

The following video is in German language, but English subtitles are available.

Erforderlicher Haftreibungskoeffizient für Gleichgewichtszustand - Technische Mechanik 1, Übung 24
Equilibrium of forces for the whole system
Equilibrium of forces for the whole system
Due to the symmetry, only the left side is considered here,
the height of the sliding blocks is neglected
Balance of forces in the x direction

\[\tag{1} 0={F_S} \sin{\left( \alpha \right) }-{F_x}\]

Balance of forces in the y direction

\[\tag{2} 0={F_y}-{F_S} \cos{\left( \alpha \right) }\]

Relationship between normal force and transversal force

\[\tag{3} {F_x}={F_y} {µ_0}\]

Resulting rope force S from G

\[\tag{4} {F_S} \cos{\left( \alpha \right) }=\frac{G}{2}\]

\[\tag{5} {F_S}=\frac{G}{2 \cos{\left( \alpha \right) }}\]

used in the balance of forces in the x direction

\[\tag{6} 0=\frac{G \sin{\left( \alpha \right) }}{2 \cos{\left( \alpha \right) }}-{F_x}\]

solve for Fx

\[\tag{7} {F_x}=\frac{G \sin{\left( \alpha \right) }}{2 \cos{\left( \alpha \right) }}\]

Solve the balance of forces in y-direction for Fy and substitute FS

\[\tag{8} {F_y}={F_S} \cos{\left( \alpha \right) }\]

\[\tag{9} {F_y}=\frac{G}{2}\]

Equation 3 yields

\[\tag{10} {µ_0}=\frac{{F_x}}{{F_y}}\]

with Fy from equation 9

\[\tag{11} {µ_0}=\frac{2 {F_x}}{G}\]

and Fx from equation 7 we get finally the minimum value for µ0

\[\tag{12} {µ_0}=\frac{\sin{\left( \alpha \right) }}{\cos{\left( \alpha \right) }}\]

or converted to

\[\tag{13} {µ_0}=\tan{\left( \alpha \right) }\]