This exercise is about the appliance of the belt friction formula (here is an online belt friction calculation tool).
Task
The band brake shown should be operated right-turning and left-turning. What is the maximum holding torque in right-turning and left-turning rotation without the brake drum rotating?
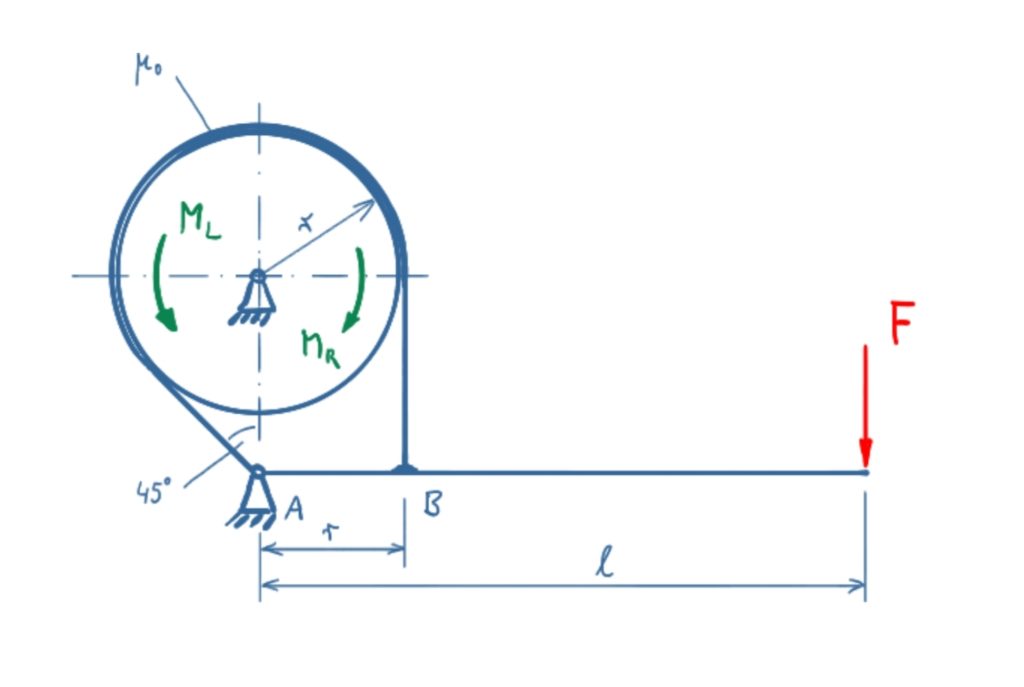
Solution
A solution video will be published soon on this channel.
The first step is the free-cut of the operator lever. The force FS doesn't have a real impact here, but it is included for formal reasons.
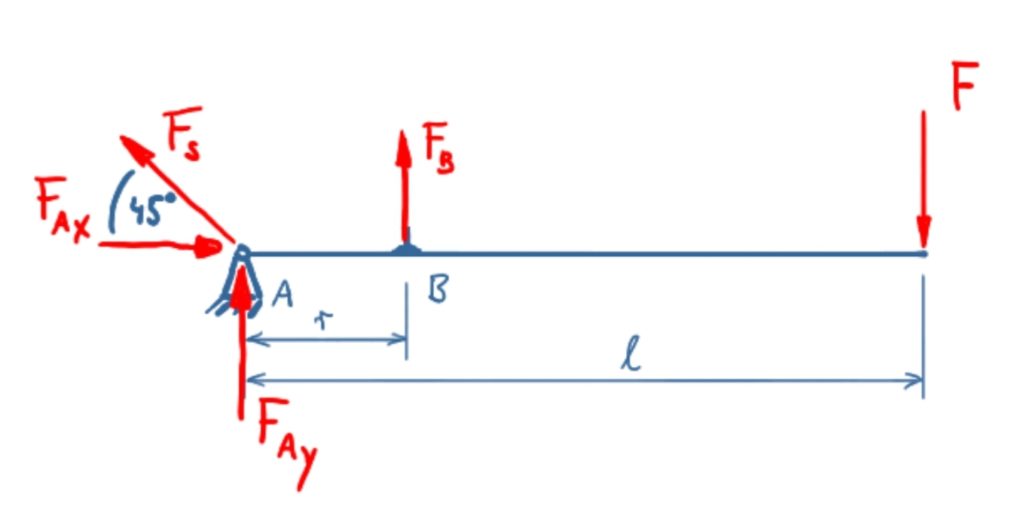
The balance of forces in x-direction is
\[ \tag{1} \sum F_x = 0 = F_{Ax} - F_S \cdot \cos 45° \]
The balance of forces in y-direction is
\[ \tag{2} \sum F_y = 0 = F_{Ay} + F_S \cdot \sin 45° + F_B - F \]
Both balances don't yield useful informations, but the balance of moments around A gives
\[ \tag{3} \sum M(A) = 0 = F_B \cdot r - F \cdot l \]
\[ \tag{4} F_B = \frac{F \cdot l}{r} \]
Next, the relationship between the rope force FS and the braking force FB is noted using the rope friction formula (Euler-Eytelwein). This is done separately for the two different directions of rotation.
Right-turning
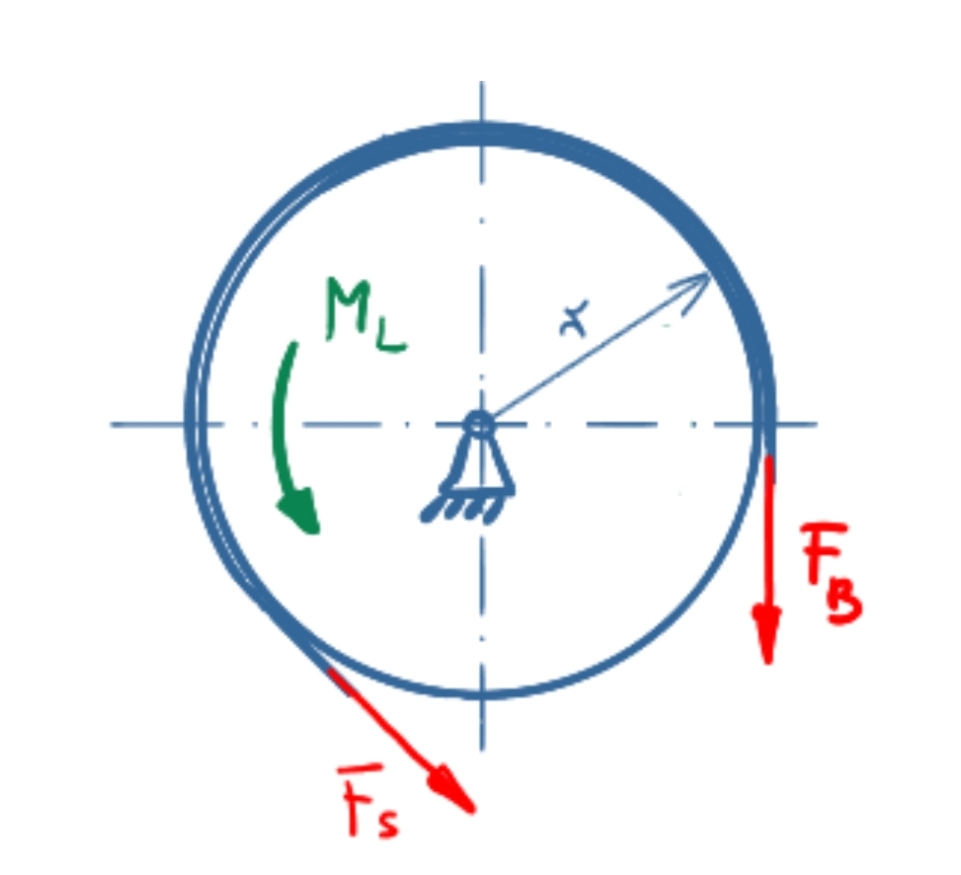
In the case of the left-turning moment, F B lies in the strained strand, F S in the loose strand. The following applies:
\[ \tag{5} F_B \leq F_S \cdot e^{µ \cdot \alpha} \]
\[ \tag{6} F_S \geq F_B \cdot e^{-µ \cdot \alpha} \]
In union with the equilibrium of moments around the drum pivot, it follows:
\[ \tag{7} \sum M = 0 = F_S \cdot r + M_L - F_B \cdot r \]
\[ \tag{8} M_L = F_B \cdot r - F_S \cdot r \]
\[ \tag{9} M_L = \frac{F \cdot l}{\bcancel{r}} \cdot \bcancel{r} - \frac{F \cdot l}{\bcancel{r}} \cdot e^{-µ \cdot \alpha} \cdot \bcancel{r}\]
\[ \tag{10} M_L = F \cdot l \cdot \left( 1 - e^{-µ \cdot \alpha} \right) \]
Left-turning
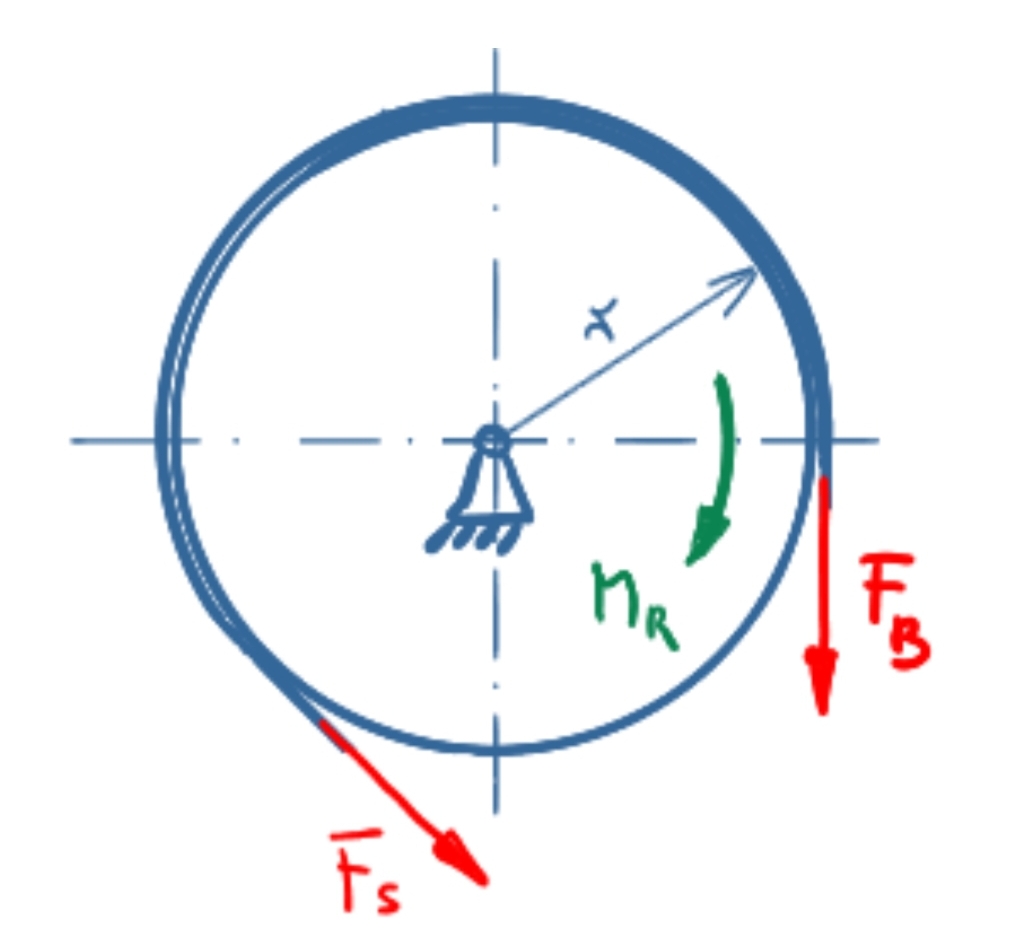
At the right-turning moment, FB lies in the loose strand, FS in the strained strand. The following applies:
\[ \tag{11} F_S \leq F_B \cdot e^{µ \cdot \alpha} \]
In union with the equilibrium of moments around the drum pivot, it follows:
\[ \tag{12} \sum M = 0 = F_S \cdot r - M_R - F_B \cdot r \]
\[ \tag{13} M_R = F_S \cdot r - F_B \cdot r \]
\[ \tag{14} M_R = \frac{F \cdot l}{\bcancel{r}} \cdot e^{µ \cdot \alpha} \cdot \bcancel{r} - \frac{F \cdot l}{\bcancel{r}} \cdot \bcancel{r} \]
\[ \tag{15} M_R = F \cdot l \cdot \left(e^{µ \cdot \alpha} - 1 \right) \]

