Werbung
Diese Übung ist Bestandteil der Aufgabensammlung Technische Mechanik II. Es wird ein Träger mit dreieckförmiger Streckenlast berechnet und folgende Fragen behandelt:
- Wie berechnet man die Lagerreaktionen bei einer dreieckförmigen Streckenlast?
- Wie berechnet man die Schnittgrößen bei einer Dreieckslast?
Aufgabe
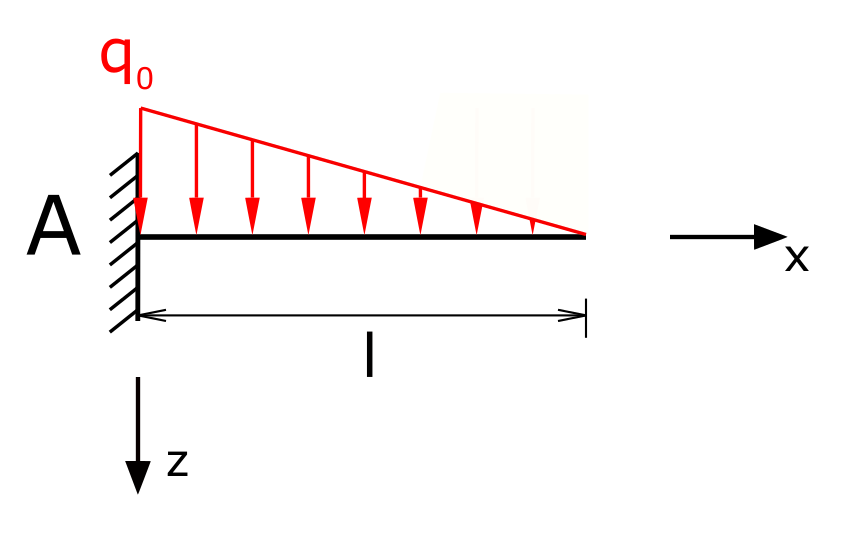
Ein einseitig fest eingespannter Träger wird wird mit einer dreieckförmigen Streckenlast belastet. Zu ermitteln sind die Beanspruchungsgrößen bzw. Schnittgrößen!
Die Funktion für die Streckenlast lautet
\[ q(x) = q_0 \cdot \left( 1 - \frac{x}{l} \right) \]
Lösung
Da der gesamte Träger von der Streckenlast belastet wird, wird keine Einteilung benötigt. Um die Schnittgrößen berechnen zu können, müssen nicht zwangsläufig die Lagerreaktionen bestimmt werden. Dies hängt davon ab, wie die Schnitte gelegt werden, d.h. also welchen Bereich des Trägers man "abschneidet". In der hier gezeigten Lösung werden die Schnitte so gelegt, dass die Lagerreaktionen nicht in den Kräftegleichgewichten der Schnittgrößen enthalten sind. Dennoch werden die Lagerreaktionen hier, der Vollständigkeit halber, im ersten Schritt berechnet.
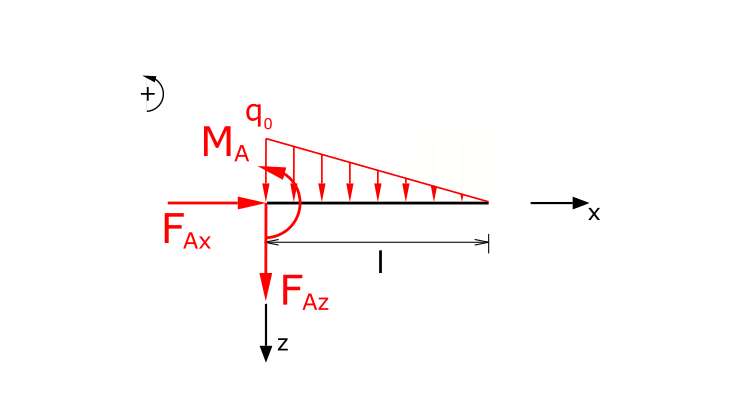
Das Aufstellen der Kräftegleichgewichte in x- und z-Richtung sowie des Momentengleichgewichts (linksdrehende Momente positiv) führt zu:
\[ \tag{1} \sum F_x = 0 = F_{Ax} \]
\[ \tag{2} \sum F_z = 0 = F_{Az} +\int_{0}^{l}{q_0 \cdot \left( 1 - \frac{x}{l} \right)\,dx} \]
\[ \tag{3} \sum M(A) = 0 = M_A - \int_{0}^{l}{q_0 \cdot \left( 1 - \frac{x}{l} \right) \cdot x\,dx} \]
Die Lagerreaktionen der festen Einspannung lassen sich damit unmittelbar bestimmen und betragen
\[ \tag{4} F_{Ax} = 0 \]
\[ \tag{5} F_{Az} = - \frac{q_0 \cdot l}{2} \]
\[ \tag{6} M_A = \frac{q_0 \cdot l^2}{6} \]
Bestimmung der Schnittgrößen
Querkräfte werden im Folgenden als Q bezeichnet, Normalkräfte als N und Biegemomente mit Mb.
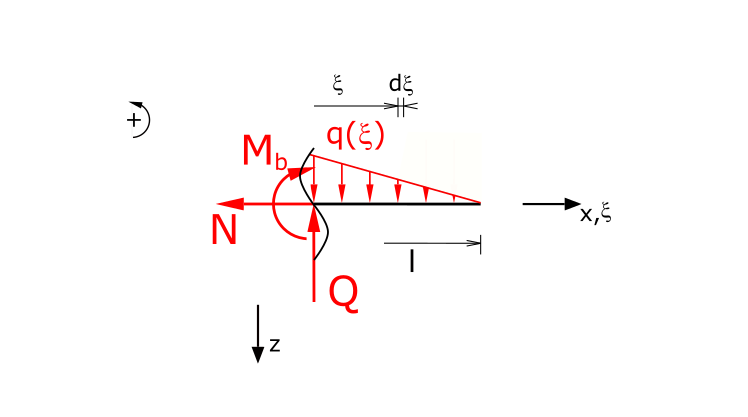
Aufstellen der Kräftegleichgewichte in x- und z-Richtung sowie des Momentengleichgewichts (die Streckenlast wird nun über die Hilfskoordinate ξ berechnet!):
\[ \tag{7} \sum F_x = 0 = -N \]
\[ \tag{8} \sum F_z = 0 = -Q +\int_{x}^{l}{q_0 \cdot \left( 1 - \frac{\xi}{l} \right)\,d\xi} \]
\[ \tag{9} \sum M(x) = 0 = - M_b - \int_{x}^{l}{q_0 \cdot \left( 1 - \frac{\xi}{l} \right) \cdot \left(\xi - x \right) \,d\xi} \]
Die Normalkraft ist schnell ermittelt:
\[ \tag{10} N = 0 \]
Die Funktion der Querkraft ergibt sich aus
\[ \tag{11} Q = \left[ q_0 \cdot \left( \xi - \frac{\xi^2}{2 \cdot l} \right) \right]_{x}^{l} \]
\[ \tag{12} Q = q_0 \cdot \left( l - \frac{l^2}{2 \cdot l} \right) - q_0 \cdot \left( x - \frac{x^2}{2 \cdot l} \right) \]
\[ \tag{13} Q = q_0 \cdot \left( \frac{x^2-2 \cdot l \cdot x}{2 \cdot l} + \frac{l}{2} \right) \]
Und schließlich das Biegemoment:
\[ \tag{14} M_{b} = \frac{{q_0} {{x}^{3}}-3 l\, {q_0} {{x}^{2}}+3 {{l}^{2}}\, {q_0} x-{{l}^{3}}\, {q_0}}{6 l} \]
Die Funktion kann an dieser Stelle einfach überprüft werden. An der Stelle x = 0 muss das Biegemoment der Lagerreaktion MA entsprechen.
\[ \require{cancel} \]\[ \tag{15} M_{b}(x=0) = \frac{{q_0} {{0}^{3}}-3 l\, {q_0} {{0}^{2}}+3 {{l}^{2}}\, {q_0} 0-{{l}^{3}}\, {q_0}}{6 l} \]
\[ \tag{16} M_{b}(x=0) = - q_0 \cdot \frac{l^2}{6} \]
Das Ergebnis stimmt überein. Das negative Vorzeichen entsteht durch die unterschiedlich angenommenen Drehsinne für die beiden Momente.
Hier gibt es eine Übung zu einem Träger mit ansteigender Dreieckslast.
Diese Übung ist Bestandteil der Aufgabensammlung Technische Mechanik 2 - Festigkeitslehre.
Werbung




