Werbung
Diese Übung zeigt, welche Vorteile es hat, ein Stabwerk mit dem Ritter-Schnittverfahren zu berechnen und beschäftigt sich mit folgenden Fragen:
- Wie wendet man das Ritter-Schnittverfahren an?
- Wie berechnet man einzelne Stabkräfte mit geringem Aufwand?
- Wie erkennt man Nullstäbe in einem Stabwerk?
Hier gibt es eine Übung zur Berechnung eines Stabwerks im Knotenpunktverfahren. Ein FEM-Tool zur Berechnung von Stabwerken ist hier zu finden.
Aufgabe
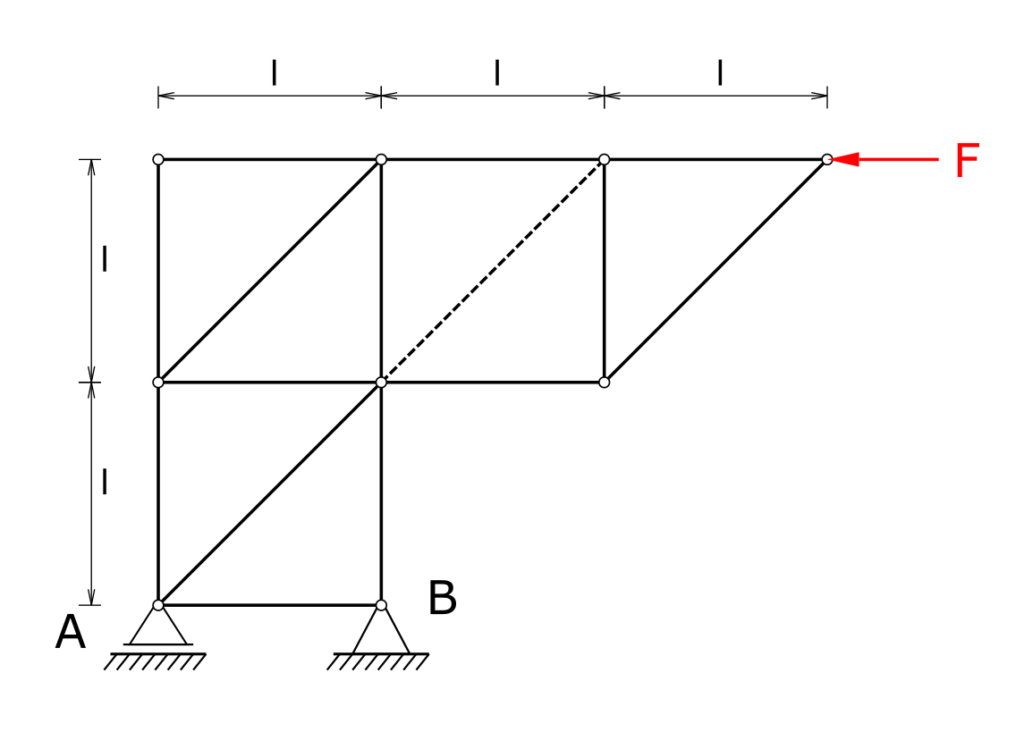
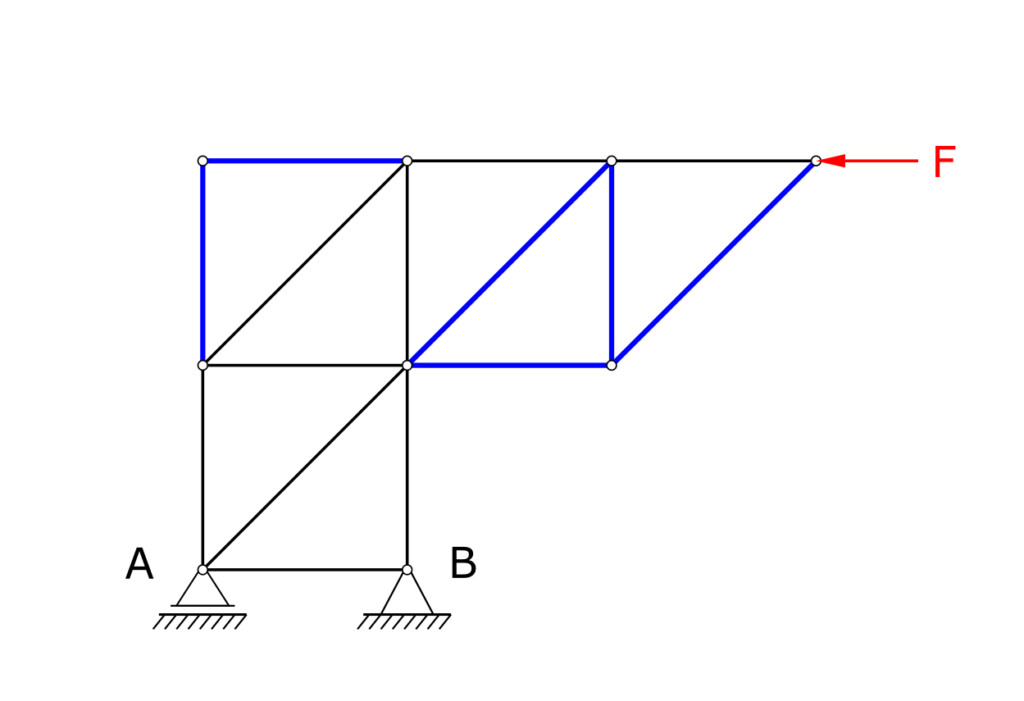
Ein Stabwerk ist in A und B gelagert und wird an seinem äußeren Ende durch eine horizontale Kraft F belastet. Das Stabwerk selbst soll als masselos angesehen werden. Zu berechnen ist die Stabkraft in dem gestrichelt dargestellten Stab! Die Nullstäbe des Stabwerks sind zu kennzeichnen!
Lösung
Für die Bestimmung der Stabkraft wird das Ritter-Schnittverfahren angewendet. Die gewählte Schnittlinie ist im folgenden Bild dargestellt. Dabei kann frei gewählt werden, welche Seite des Schnittes betrachtet wird. In der hier gezeigten Lösung wird die Seite mit den Lagerreaktionen betrachtet, was bedeutet, dass diese im ersten Schritt ermittelt werden müssen. (Um das Stabwerk mit dem Ritter-Schnittverfahren berechnen zu können, kann alternativ auch die Seite ohne die Lagerreaktionen betrachtet werden, das wird weiter unten auf der Seite gezeigt.)
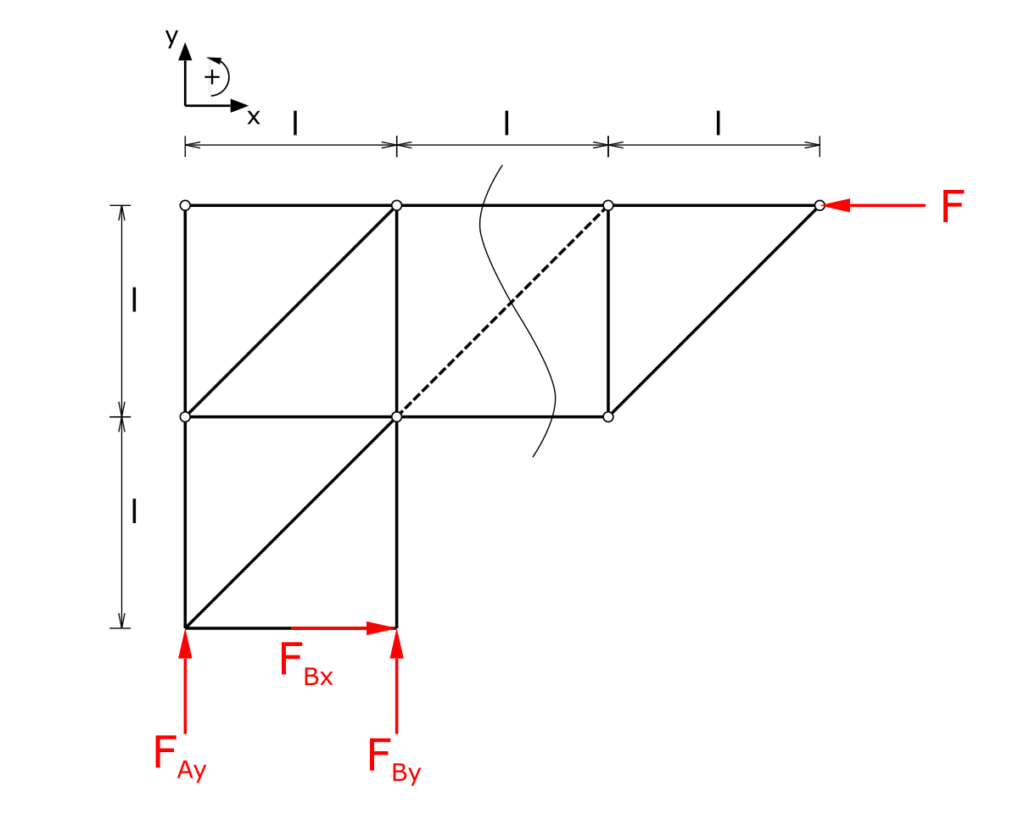
Da die Stäbe dieses Stabwerks nur horizontal, vertikal und unter dem Winkel 45° angeordnet sind, können die Ergebnisse der Winkelfunktionen in Kurzform notiert werden.
Lagerreaktionen
Aufstellen der Kräfte- und Momentengleichgewichte (linksdrehende Momente positiv):
\[ \tag{1} \sum F_x = 0 = F_{Bx} - F \]
\[ \tag{2} \sum F_y = 0 = F_{Ay} + F_{By} \]
\[ \tag{3} \sum M(A) = 0 = F_{By} \cdot l + F \cdot 2 \cdot l \]
Die Lagerreaktionen sind also
\[ \tag{4} F_{Bx} = F \]
\[ \tag{5} F_{By} = - 2 \cdot F \]
\[ \tag{6} F_{Ay} = 2 \cdot F \]
Nullstäbe, erster Schritt
Bevor der Schnitt betrachtet wird, ist es sinnvoll, die unmittelbar erkennbaren Nullstäbe zu kennzeichnen. Nullstäbe entstehen immer dann, wenn für eine bestimmte Achsenrichtung x oder y nur ein einziger Stab in einem Knoten angebunden ist. D.h. dieser Stab kann dann seine Kraft an keinen anderen Stab weitergeben.
Für das vorliegende Stabwerk trifft das auf die in der nachfolgenden Abbildung blau markierten Stäbe zu.
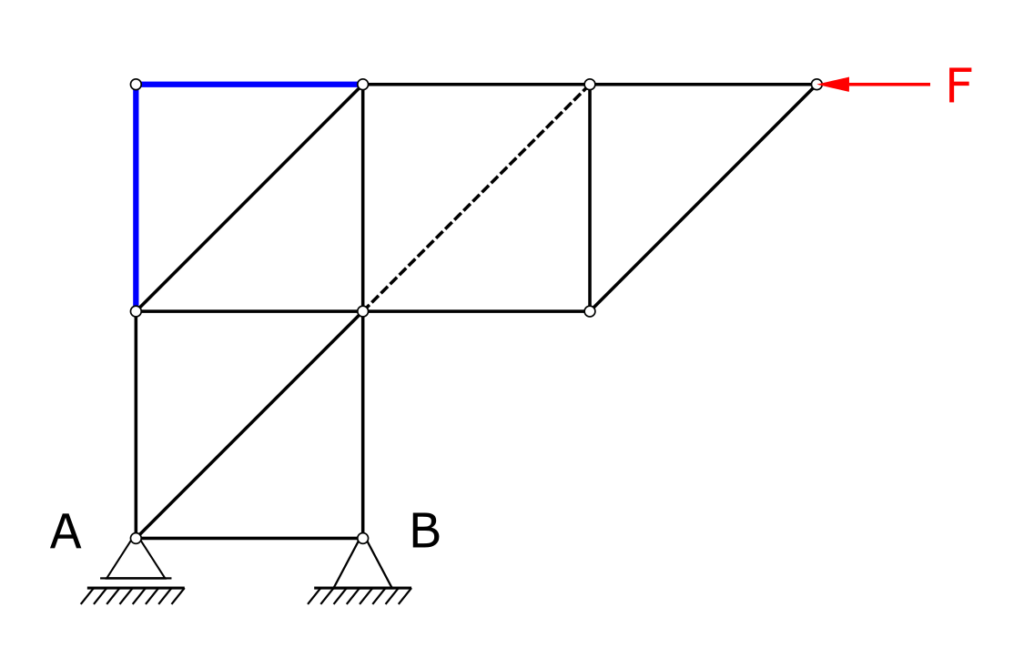
Stabkräfte
Als nächstes werden die Stabkräfte (hier als Zugkräfte) an die durchgeschnittenen Stäbe angetragen und die statischen Gleichgewichtsbedingungen aufgestellt. Der Punkt A wird als Drehpunkt gewählt.
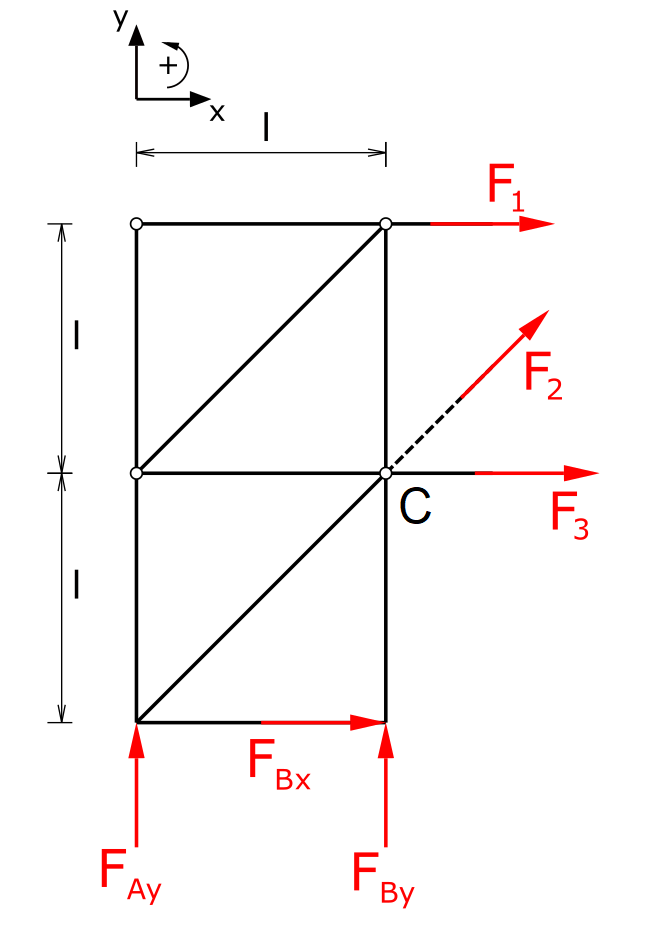
\[ \tag{7} \sum F_x = 0 = F_{Bx} + F_1 + \frac{F_2}{\sqrt{2}} + F_3 \]
\[ \tag{8} \sum F_y = 0 = F_{Ay} + F_{By} + \frac{F_2}{\sqrt{2}} \]
\[ \tag{9} \sum M(A) = 0 = F_{By} \cdot l - F_3 \cdot l - F_1 \cdot 2 \cdot l \]
Die Stabkraft F2 ist schnell ermittelt:
\[ \tag{10} F_2 = 0 \]
Es handelt sich also um einen weiteren Nullstab.
Nun werden die restlichen Stabkräfte berechnet. Man könnte die bisherigen Gleichungen umstellen und einsetzen, oder man betrachtet die Momente um Punkt C.
\[ \tag{11} \sum M(C) = 0 = F_{Bx} \cdot l - F_{Ay} \cdot l - F_1 \cdot l \]
\[ \tag{12} F_1 = -F \]
D.h. der betrachtete Stab ist ein Druckstab. Die letzte fehlende Stabkraft ergibt sich aus Gleichung 7.
\[ \tag{13} F_3 = 0 \]
Auch dieser Stab ist ein Nullstab.
Nullstäbe, zweiter Schritt
Mit den bis hierhin gefundenen Nullstäben können nun noch einmal alle Knoten des Stabwerks überprüft werden. Es ergeben sich folgende weitere Nullstäbe:
Die hohe Anzahl von Nullstäben resultiert aus der Wirkrichtung der angreifenden Kraft. D.h. wenn die angreifende Kraft eine vertikale Komponente enthält, ändert sich auch die Verteilung der Nullstäbe im Stabwerk.
Alternative Betrachtung
Wie oben bereits erwähnt, hätte man das Stabwerk mit dem Ritter-Schnittverfahren auch durch das Aufstellen des statischen Gleichgewichts für die andere Seite des Schnittes betrachten können. In dem Fall hätte der freigeschnittene Element folgendermaßen ausgesehen:
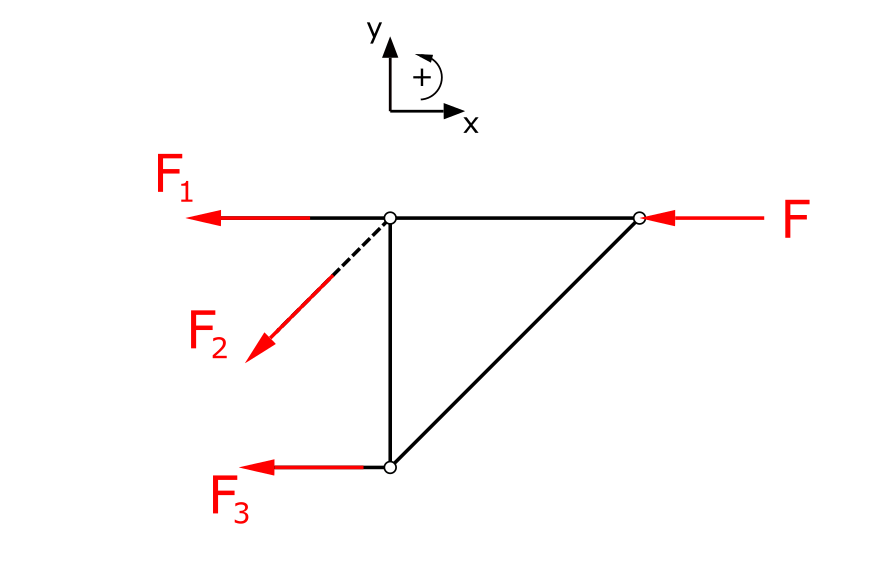
An dieser Stelle gibt es einen sehr guten Online-Rechner für Stabwerke, mit dem man seine Ergebnisse schnell überprüfen kann.
Werbung




